After a few months of not finding the time to improve the previous accuracy of the MNIST character recognition, I went along to the 1st London Kaggle Meetup.
The great thing about this is being amongst experts, and also not being distracted from getting on with it.
I had a chat with a couple of experts on image classification and it was brought to my attention that it is pretty normal for neural nets to be trained on the training dataset multiple times - epochs. I was staggered! I tried it and the results improved!
That's the massive benefit of just talking to people!
I also found the time to finally measure the accuracy of the neural network predictions against the test set - previously I had been measuring the output error as the training proceeded.
The accuracy against the training set jumped to a fantastic 97% (and later to 97.5% with 50 epochs)
Overall the results are now in line with what we should expect from a neural network - see http://yann.lecun.com/exdb/mnist/ benchmarks for different methods.
Saturday 22 August 2015
Wednesday 13 May 2015
Recognising Handwritten Characters
Having got a small neural network to learn logical XOR I tried scaling up to learn the MNIST handwritten characters.
The early rough code is here: www.googledrive.com/host/0B6e9Zx7axvo-TjcwM2J5cUlVLVk/
You'll recall the images are bitmaps of 28x28 pixels. The neural network therefore has 28x28 = 784 nodes. That's a big step up from our 2 or 3 nodes!
The output needs to represent the range of possible answers, and one way of doing this is simply to have a node for each answer - ie 10 nodes, one for each possible character between 0 and 9.
The number of middle hidden layer nodes is interesting - it could be 784, more than 784, or a lot less. More means great computational load and perhaps a risk of over-fitting. Too few and the neural network cannot learn to classify the characters because there isn't enough freedom to represent the model required. Let's try 100 nodes.
Look through the code and you'll see the code
inputs = (numpy.asfarray(linebits[1:])/ 256.0) + 0.01
which scales the inputs fom the initial range of 0-255 to the range 0.01 to just over 1.00. We could fix this to make it exactly one but this is just a quick hack to prevent the input having an input of zero which we know damages back propagation learning.
The code runs through all 60,000 training examples - character bitmaps together with the correct previously known answer. As we do this we keep a track of the sum-squared-error and redirect it to a file for plotting later. Just like in the previous posts, we expect it to fall over training epoch. But it doesn't look like a clean drop like we've seen before.
You might be able to see a density of points shifting downwards which we need a better way of visualising. Let's plot these errors as a histogram. The following gnuplot code does this:
binwidth=0.1
plot [:][:] 'a.txt' using (bin($1,binwidth)):(1.0) smooth freq with boxes
Now that's much clearer! The vast majority of sum-square-errors are in the range 0.0 - 0.1. In fact approx 48,000 of the 60,000 or 80% of them are. That's a very good result for a first attempt at training a neural network to recognise handwritten numerals.
Test Query
The last bit of code in the Python notebook illustrates querying the neural network. In this case we take the 5th example (it could have been any other example) which represents the numeral "2". Some code prepares the query and we see the following output:
finaloutputs =
[[ 1.31890673e-05]
[ 8.37041536e-08]
[ 9.96541147e-01]
[ 1.68720831e-06]
[ 1.39223748e-07]
[ 8.52160977e-09]
[ 3.48925352e-06]
[ 4.08379490e-05]
[ 4.82287514e-05]
[ 5.91914796e-03]]
These are the ten output layer nodes. We can see that the largest one by far is the 3rd element which represents the desired "2" - because we count from zero: 0, 1, 2, ...Let's visualise these output values:
You can see quite clearly the output value for the node representing "2" is by far the largest! The next most likely candidate "9" has an output 100 times smaller.
The early rough code is here: www.googledrive.com/host/0B6e9Zx7axvo-TjcwM2J5cUlVLVk/
You'll recall the images are bitmaps of 28x28 pixels. The neural network therefore has 28x28 = 784 nodes. That's a big step up from our 2 or 3 nodes!
The output needs to represent the range of possible answers, and one way of doing this is simply to have a node for each answer - ie 10 nodes, one for each possible character between 0 and 9.
The number of middle hidden layer nodes is interesting - it could be 784, more than 784, or a lot less. More means great computational load and perhaps a risk of over-fitting. Too few and the neural network cannot learn to classify the characters because there isn't enough freedom to represent the model required. Let's try 100 nodes.
Look through the code and you'll see the code
inputs = (numpy.asfarray(linebits[1:])/ 256.0) + 0.01
which scales the inputs fom the initial range of 0-255 to the range 0.01 to just over 1.00. We could fix this to make it exactly one but this is just a quick hack to prevent the input having an input of zero which we know damages back propagation learning.
The code runs through all 60,000 training examples - character bitmaps together with the correct previously known answer. As we do this we keep a track of the sum-squared-error and redirect it to a file for plotting later. Just like in the previous posts, we expect it to fall over training epoch. But it doesn't look like a clean drop like we've seen before.
You might be able to see a density of points shifting downwards which we need a better way of visualising. Let's plot these errors as a histogram. The following gnuplot code does this:
binwidth=0.1
plot [:][:] 'a.txt' using (bin($1,binwidth)):(1.0) smooth freq with boxes
Now that's much clearer! The vast majority of sum-square-errors are in the range 0.0 - 0.1. In fact approx 48,000 of the 60,000 or 80% of them are. That's a very good result for a first attempt at training a neural network to recognise handwritten numerals.
Test Query
The last bit of code in the Python notebook illustrates querying the neural network. In this case we take the 5th example (it could have been any other example) which represents the numeral "2". Some code prepares the query and we see the following output:
finaloutputs =
[[ 1.31890673e-05]
[ 8.37041536e-08]
[ 9.96541147e-01]
[ 1.68720831e-06]
[ 1.39223748e-07]
[ 8.52160977e-09]
[ 3.48925352e-06]
[ 4.08379490e-05]
[ 4.82287514e-05]
[ 5.91914796e-03]]
These are the ten output layer nodes. We can see that the largest one by far is the 3rd element which represents the desired "2" - because we count from zero: 0, 1, 2, ...Let's visualise these output values:
You can see quite clearly the output value for the node representing "2" is by far the largest! The next most likely candidate "9" has an output 100 times smaller.
Tuesday 5 May 2015
Saturation and Normalising Inputs
I've been puzzled by my neural network code not working. It struck me that back propagation suffers some issues, like getting struck in local minima, or not being able to learn from inputs that are all the same, or zero.
I think I was suffering from network saturation - where the activation functions were all at the point where the gradient is almost zero. No gradient means no weight change means no learning!
The simple problem I was trying to get working was the famous XOR problem. Normalising the inputs from the range [0, 1.0] to [0.1, 0.9] seems to work much better.
The python source code I have so far is at:
The resultant sum-squared-error for XOR learning is:
I will read with interest the fantastic paper "Efficient Backprop": http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf
I tried my early code with OR, and AND not just XOR and it all worked!
I'm still cautious so I'll think about this a bit more and read that paper in more detail.
I think I was suffering from network saturation - where the activation functions were all at the point where the gradient is almost zero. No gradient means no weight change means no learning!
The simple problem I was trying to get working was the famous XOR problem. Normalising the inputs from the range [0, 1.0] to [0.1, 0.9] seems to work much better.
The python source code I have so far is at:
The resultant sum-squared-error for XOR learning is:
I will read with interest the fantastic paper "Efficient Backprop": http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf
I tried my early code with OR, and AND not just XOR and it all worked!
I'm still cautious so I'll think about this a bit more and read that paper in more detail.
Sunday 3 May 2015
Hill Climbing Learning
Having real trouble debugging my back propagation algorithm, and also understanding the error in my own derivation of weight change... so took a step back and tried a different approach altogether.
Hill climbing is a fancy term but all we're doing is taking an untrained neural network and making a small change to one of the weights to see if it improves the overall result. If it does, keep that change, if it doesn't discard it and revert.
That's an intuitive explanation - much easier to understand than back propagation at the weight change level.
Why is it called hill climbing? Imagine the landscape of weights .. 2-dimensions is easy to imagine .. that is w1 and w2. We stand at a starting position and we want to find the best w1 and w2. If we take a small step in a random direction, we can then see if it improves the overall output (squared sum error) of the neural network - or not. If it does, you've moved closer to the optimal w1, w2. Keep doing this and you'll get there. The "hill" is a sense of solution quality, the error function for example.
Again - a great graph showing a neural network improving it's accuracy over training epochs:
Do keep in mind that is method, just like the back propagation, can end up with a locally - not globally - optimum solution. Thinking of that landscape above, we end up in a ditch but not the deepest ditch!
Hill climbing is a fancy term but all we're doing is taking an untrained neural network and making a small change to one of the weights to see if it improves the overall result. If it does, keep that change, if it doesn't discard it and revert.
That's an intuitive explanation - much easier to understand than back propagation at the weight change level.
Why is it called hill climbing? Imagine the landscape of weights .. 2-dimensions is easy to imagine .. that is w1 and w2. We stand at a starting position and we want to find the best w1 and w2. If we take a small step in a random direction, we can then see if it improves the overall output (squared sum error) of the neural network - or not. If it does, you've moved closer to the optimal w1, w2. Keep doing this and you'll get there. The "hill" is a sense of solution quality, the error function for example.
Again - a great graph showing a neural network improving it's accuracy over training epochs:
Do keep in mind that is method, just like the back propagation, can end up with a locally - not globally - optimum solution. Thinking of that landscape above, we end up in a ditch but not the deepest ditch!
Saturday 18 April 2015
Backpropagation Video Tutorials
The following youtube videos are a great tutorial on the backpropagation algorithm. They're about 13 minutes each.
Enjoy! Amd credit to Ryan Harris.
Enjoy! Amd credit to Ryan Harris.
Wednesday 15 April 2015
Early Code Seems to Work
I've been working on turning the theory of the last few posts into working code. The hardest part has been trying to create code that works with matrices as a whole - and not code which inefficiently works element by element.
Today I was a happy milestone! The code is far from finished but I did my first cut of the back propagation updating the weights.
To check this works, my code prints out lots of info on internal variables, like the weights or the outputs of the hidden layer, or the final output. I used the output of the overall network error - which is the difference between the training target and the actual output of the network to see if it got smaller for each iteration of the back propagation (called epoch).
I was delighted to see it did:
The code is still early, and the above example used a very simplistic training set (all 1s as input and a 1 as output for a 3-2-1 node nework) but the fact that the overall error falls with training epoch is a very good sign.
Onwards and upwards.
Next steps ... I'm worried my code doesn't handle the division in the weight update equation well if the denominator is small or zero:
Friday 10 April 2015
Matrices - Doing Lot of Work in One Go
One of the things that programmers and algorithm designers try to do is to take advantage of that fact that computers are quite good at doing lots of the same thing very quickly.
What do we mean by this?
Imagine I had a list of bank balances and I wanted to multiply them by 1.1 to add 10% interest. I could do it by taking each one individually and adding the 10%. Something like:
For each balance in bank:
newbalance = b * 1.10
pass
However - many computers, and programming languages running on those computers, allow the same job to be done on chunks of many data items. This is vastly more efficient (and quicker) than looping over each data item. This would look something like this:
newbalance = balance * 1.10
The underlining shows the thing is a matrix. Thislast expression allows the computer to operate on all of the balance data items at the same time, paralellising the calculation. Its as if the computer gives the work to a team of workers, instead of getting one worker to work through the list sequentially. In reality, there is a limit to how much this parallisation happens, but in most cases it is vastly more efficient.
This is variously called parallelisation, array programming, vectorisation. Wikipedia has a good entry on it http://en.wikipedia.org/wiki/Array_programming
Now... it is worth exploring to see if this is applicable to our neural network calculations.
In fact calculating the outputs of each neural network layer easily translates into this vectorised approach.
Consider the calculation of outputs from the output layer using the outputs from the hiden layer and of course taking into account the weights.
output_1 = activation_function ( hiddenoutput_1 * weight_11 + hiddenoutput_2 * weight_21 + hiddenoutput_3 * weight_31 )
output_2 = activation_function ( hiddenoutput_1 * weight_12 + hiddenoutput_2 * weight_22 + hiddenoutput_3 * weight_32 )
...
Can you see the pattern? Look at the drawing connecting the hidden layer to the output layer through the weights. Let's user shorter words to see it cleaer:
o_1 = af ( ho_1 * w_11 + ho_2 * w_21 + ho_3 * w_31 )
o_2 = af ( ho_1 * w_12 + ho_2 * w_22 + ho_3 * w_32 )
...
These patterns where you can see essentially the same expressions but with just one array index changing are usually emanable to vectorisation. It doesn't take long to see that:
So when we're implementing this in Python we can use the dot product function to multiply the weights array and the hidden outputs array. The same logic applies to arraive at the hidden outputs using the inputs and their associated weights.
Neat!
That's the forward flow vectorised.... but I'm still struggling to parallelise the backpropagation that we talked about in the last post.
What do we mean by this?
Imagine I had a list of bank balances and I wanted to multiply them by 1.1 to add 10% interest. I could do it by taking each one individually and adding the 10%. Something like:
For each balance in bank:
newbalance = b * 1.10
pass
However - many computers, and programming languages running on those computers, allow the same job to be done on chunks of many data items. This is vastly more efficient (and quicker) than looping over each data item. This would look something like this:
newbalance = balance * 1.10
The underlining shows the thing is a matrix. Thislast expression allows the computer to operate on all of the balance data items at the same time, paralellising the calculation. Its as if the computer gives the work to a team of workers, instead of getting one worker to work through the list sequentially. In reality, there is a limit to how much this parallisation happens, but in most cases it is vastly more efficient.
This is variously called parallelisation, array programming, vectorisation. Wikipedia has a good entry on it http://en.wikipedia.org/wiki/Array_programming
Now... it is worth exploring to see if this is applicable to our neural network calculations.
In fact calculating the outputs of each neural network layer easily translates into this vectorised approach.
Consider the calculation of outputs from the output layer using the outputs from the hiden layer and of course taking into account the weights.
output_1 = activation_function ( hiddenoutput_1 * weight_11 + hiddenoutput_2 * weight_21 + hiddenoutput_3 * weight_31 )
output_2 = activation_function ( hiddenoutput_1 * weight_12 + hiddenoutput_2 * weight_22 + hiddenoutput_3 * weight_32 )
...
Can you see the pattern? Look at the drawing connecting the hidden layer to the output layer through the weights. Let's user shorter words to see it cleaer:
o_1 = af ( ho_1 * w_11 + ho_2 * w_21 + ho_3 * w_31 )
o_2 = af ( ho_1 * w_12 + ho_2 * w_22 + ho_3 * w_32 )
...
These patterns where you can see essentially the same expressions but with just one array index changing are usually emanable to vectorisation. It doesn't take long to see that:
Neat!
That's the forward flow vectorised.... but I'm still struggling to parallelise the backpropagation that we talked about in the last post.
Friday 3 April 2015
Backpropagation 3/3
In the last two posts on backpropagation we saw:
We now need to cover two more themes:
Sigmoid Activation Function
We know the activation function needs to meet certain criteria. These are
For this last reason, the sigmoid function is often used. Really, the main reason for it is easy calculus and it has the right shape (ramping from a lower level to a higher level), not much more!
What is this easy calculus? Well if the sigmoid function is
then the derivative
Nice and neat! You could work this out using all the algebra but that's too boring for a blog - you see the few steps of algebra here.
But we actually want the relationship between the output f and the weights aka Δf/Δw. That's ok - and easy - because the weights are independent of each other. The "x" in f(x) is really the weighted sum of several inputs w1*x1 + w2*x2 + w3*x3 + ... and so on. The nice thing about calculus is that the derivative of f with respect to one of these, say w2, is independent of anything else including the other wn.
If we have Δf/Δx but we want Δf/Δw what do we do? Well, we use the "chain rule" of calculus which helps us do this translation:
This looks like a normal fraction relationship but isn't really - but if it helps you remember it, thats ok.
CORRECTION: This post has been edited to remove the previous content of this section. You can find a fuller explanation of the maths, still written in an accessible manner, here in the early draft of Make Your Own Neural Network:
http://makeyourownneuralnetwork.blogspot.co.uk/2016/02/early-draft-feedback-wanted.html
What error do you use for internal nodes?
I forgot to explain a key point. The error of the entire neural network is easy to understand - its the difference between the output of the network and the desired target output. We use this to refine the final layer of nodes using the above formula.
But what about internal nodes? It doesn't make sense for the internal nodes to to be refined using the same formula but with the error of the entire network. Intuitively they all have smaller errors that contribute - the final error is too big. What do we do?
We could simply divide the big final error equally into the number of nodes. Not too bad an idea but that wouldn't reflect the contribution of some weights taking the final output in different directions - negative not positive weights. If a weight was trying to invert its input, it doesn't make sense to naively distribute the final error without taking this into account. This is a clue to a better approach.
That better approach is to divide the final error into pieces according to the weights. This blog talks about it http://home.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html but the idea is easily illustrated:
The error is divided between nodes C and E in the same proportion as WCF and WEF. The same logic applies to dividing this error at A and B. The error used to calculate updated WAC and WBC is the error at WCF divided in the proportion WAC to WBC .
What does this mean? It means that if, say WCF was much larger than WEF it should carry much more of the final error. Which is nicely intuitive too!
Again - it's amazing how few texts and guides explain this, leaving it a mystery.
- that the error of a neutral network is used to refine the internal weights
- that simple calculus is used to determine the change in weight for a single neuron
We now need to cover two more themes:
- activation functions that have nice properties to support this calculus
- seeing how this change in weights is applied to internal layers of a neural network, and to many nodes each with many connections
Sigmoid Activation Function
We know the activation function needs to meet certain criteria. These are
- it must be non-linear, otherwise the entire neural network collapses into a single linear node
- it should be broadly similar to biology - that is be monotonically increasing and reflect "activation" or "firing" once a threshold of inputs is reached
For this last reason, the sigmoid function is often used. Really, the main reason for it is easy calculus and it has the right shape (ramping from a lower level to a higher level), not much more!
What is this easy calculus? Well if the sigmoid function is
f(x) = 1/(1+exp(-x))
then the derivative
Δf/Δx is amazingly simple f(x)(1-f(x)).
Nice and neat! You could work this out using all the algebra but that's too boring for a blog - you see the few steps of algebra here.
But we actually want the relationship between the output f and the weights aka Δf/Δw. That's ok - and easy - because the weights are independent of each other. The "x" in f(x) is really the weighted sum of several inputs w1*x1 + w2*x2 + w3*x3 + ... and so on. The nice thing about calculus is that the derivative of f with respect to one of these, say w2, is independent of anything else including the other wn.
If we have Δf/Δx but we want Δf/Δw what do we do? Well, we use the "chain rule" of calculus which helps us do this translation:
Δf/Δw is the same as Δf/Δx * Δx/Δw
This looks like a normal fraction relationship but isn't really - but if it helps you remember it, thats ok.
CORRECTION: This post has been edited to remove the previous content of this section. You can find a fuller explanation of the maths, still written in an accessible manner, here in the early draft of Make Your Own Neural Network:
http://makeyourownneuralnetwork.blogspot.co.uk/2016/02/early-draft-feedback-wanted.html
What error do you use for internal nodes?
I forgot to explain a key point. The error of the entire neural network is easy to understand - its the difference between the output of the network and the desired target output. We use this to refine the final layer of nodes using the above formula.
But what about internal nodes? It doesn't make sense for the internal nodes to to be refined using the same formula but with the error of the entire network. Intuitively they all have smaller errors that contribute - the final error is too big. What do we do?
We could simply divide the big final error equally into the number of nodes. Not too bad an idea but that wouldn't reflect the contribution of some weights taking the final output in different directions - negative not positive weights. If a weight was trying to invert its input, it doesn't make sense to naively distribute the final error without taking this into account. This is a clue to a better approach.
That better approach is to divide the final error into pieces according to the weights. This blog talks about it http://home.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html but the idea is easily illustrated:
What does this mean? It means that if, say WCF was much larger than WEF it should carry much more of the final error. Which is nicely intuitive too!
Again - it's amazing how few texts and guides explain this, leaving it a mystery.
Sunday 15 March 2015
Backpropagation Part 2/3
This post continues from Part 1/3, and aims to explain in more detail how each weight in a neural network is refined during it's training.
Last time we covered the overarching idea that, during training, the network's overall output error is the key thing that guides how each internal weight must be tuned so that the overall output error is reduced.
Simpler Case First: Linear Neuron
Because the maths usually gets in the way of most explanations, let's illustrate the idea using an simpler model of a neuron.
Remember the neuron we described in an earlier post? We know consider an artificially simple node which has a linear activation function. Linear means the output function is of the form ax+b .... that is, (weight x input) + constant, or o=w.i+c to be more concise.
Ignore for now the fact that useful neural networks can't have such simple activation functions.
Imagine we start with an untrained neuron, with
So what do we do with this error -1.8? We said in the last post that this is the value we used to refine the network's weights to improve the result.
Derivatives: How Outputs Depend on Other Factors
To answer this we need to dig a little into the activation function which turns the input into the output and uses the weight to do so. This makes intuitive sense - if we're to tweak the weight, we need to understand the function which uses the weight to produce, hopefully, a better output. This function is of course the activation function o = w.i + c.
Look at the following graphs showing o = w.i for different w. Larger w have larger slopes, negative w have slopes going in the oppositve direction. So w has a direct effect on the output. You can see that w=-0.7 would be a better weight for our training dara because with this the output would be -0.7, not so far from the desired -1.0. Much better than 0.8 above.
But we need to be able to express this connection more precisely than handwaving at a graph.
As is all too common in mathematics, you can get an insight into a function by looking at how it depends on a variable.You'll remember this is simply calculus - how does X change as a result of Y changing. The following shows the idea applied to a general activation function.
So let's do this with o = w.i + c and see how it varies with w, because we're interested in tweaking w. The derivative of o with respect to w is Δo/Δw and is simply Δo/Δw = i. This is simple school level calculus.
Let's rearrange that expression so that we have the output and weights on different sides of the equation. That becomes Δo = Δw.i and this simply says that a small change in w multiplied by i gives the small change in o. Or rearranging slightly Δw = Δo/i.
This is looking hopeful! The Δw is the change in weight we want to work out. We know i because for the training data set it was 1.0. So what is Δo? It is the change in o, the output, we want to correspond with that change in w. But what should Δo be? Its the error, the different between the desired and current output. So, using the above training data item, we have error = Δo = -1.8. This deliberately simplistic function and it's derivative tell us that the Δw should change by -1.8 too. The weight w was 0.8 but changing it by -1.8 gives the new value -1.0.
Hey presto! The new weight of -1.0, gives us a new improved output of -1.0 ... to perfectly match the target desired output.
Step Back: The Process
Ok - phew! That was along winded way of tweaking a really simple weight to get a better output... but the important thing is the process - the process of using the derivatives of the activation function to understand how the output depends on the weight. Or more precisely, how small changes in output correlate to changes in weight Δw. And using this relationship to work out Δw, the required weight change.
This is the important idea: That we improve the weights by calculating the small change dw based on the desired change in output, Δo. And the relationship between Δw and Δo is derived using calculus of the activation function.
Moderation
In reality, we don't just change the weight by the value of Δw. Instead we moderate how much of the Δw change we apply. This is often called a learning rate. We might choose to only apply half of each Δw we calculate for example. Why do this?
We moderate the "training", or changes in weight recommended by the calculation of Δw, because the training data won't necessarily perfectly fit a real world model, and trying to aim at it too strongly means risking over-fitting. Over-fitting is when a system is too closely matched to imperfect training data, and as a result performs badly on new data. In short, it doesn't generalise but merely memorises the training data.
Next Time
This time we looked at a deliberately and extremely simple neural network consisting of one neuron, and a simple activation function, just to see more clearly how we can refine the weights with each training example.
Next time we'll have to work out how to do this with a more complex network, with hidden layers.
Last time we covered the overarching idea that, during training, the network's overall output error is the key thing that guides how each internal weight must be tuned so that the overall output error is reduced.
Simpler Case First: Linear Neuron
Because the maths usually gets in the way of most explanations, let's illustrate the idea using an simpler model of a neuron.
Remember the neuron we described in an earlier post? We know consider an artificially simple node which has a linear activation function. Linear means the output function is of the form ax+b .... that is, (weight x input) + constant, or o=w.i+c to be more concise.
Ignore for now the fact that useful neural networks can't have such simple activation functions.
Imagine we start with an untrained neuron, with
- weight w=0.8
- and for simplicity set the constant c as zero.
- Imagine also we have a training data with input = 1.0 and output = -1.0.
So what do we do with this error -1.8? We said in the last post that this is the value we used to refine the network's weights to improve the result.
Derivatives: How Outputs Depend on Other Factors
To answer this we need to dig a little into the activation function which turns the input into the output and uses the weight to do so. This makes intuitive sense - if we're to tweak the weight, we need to understand the function which uses the weight to produce, hopefully, a better output. This function is of course the activation function o = w.i + c.
Look at the following graphs showing o = w.i for different w. Larger w have larger slopes, negative w have slopes going in the oppositve direction. So w has a direct effect on the output. You can see that w=-0.7 would be a better weight for our training dara because with this the output would be -0.7, not so far from the desired -1.0. Much better than 0.8 above.
But we need to be able to express this connection more precisely than handwaving at a graph.
As is all too common in mathematics, you can get an insight into a function by looking at how it depends on a variable.You'll remember this is simply calculus - how does X change as a result of Y changing. The following shows the idea applied to a general activation function.
So let's do this with o = w.i + c and see how it varies with w, because we're interested in tweaking w. The derivative of o with respect to w is Δo/Δw and is simply Δo/Δw = i. This is simple school level calculus.
Let's rearrange that expression so that we have the output and weights on different sides of the equation. That becomes Δo = Δw.i and this simply says that a small change in w multiplied by i gives the small change in o. Or rearranging slightly Δw = Δo/i.
This is looking hopeful! The Δw is the change in weight we want to work out. We know i because for the training data set it was 1.0. So what is Δo? It is the change in o, the output, we want to correspond with that change in w. But what should Δo be? Its the error, the different between the desired and current output. So, using the above training data item, we have error = Δo = -1.8. This deliberately simplistic function and it's derivative tell us that the Δw should change by -1.8 too. The weight w was 0.8 but changing it by -1.8 gives the new value -1.0.
Hey presto! The new weight of -1.0, gives us a new improved output of -1.0 ... to perfectly match the target desired output.
Step Back: The Process
Ok - phew! That was along winded way of tweaking a really simple weight to get a better output... but the important thing is the process - the process of using the derivatives of the activation function to understand how the output depends on the weight. Or more precisely, how small changes in output correlate to changes in weight Δw. And using this relationship to work out Δw, the required weight change.
This is the important idea: That we improve the weights by calculating the small change dw based on the desired change in output, Δo. And the relationship between Δw and Δo is derived using calculus of the activation function.
Moderation
In reality, we don't just change the weight by the value of Δw. Instead we moderate how much of the Δw change we apply. This is often called a learning rate. We might choose to only apply half of each Δw we calculate for example. Why do this?
We moderate the "training", or changes in weight recommended by the calculation of Δw, because the training data won't necessarily perfectly fit a real world model, and trying to aim at it too strongly means risking over-fitting. Over-fitting is when a system is too closely matched to imperfect training data, and as a result performs badly on new data. In short, it doesn't generalise but merely memorises the training data.
Next Time
This time we looked at a deliberately and extremely simple neural network consisting of one neuron, and a simple activation function, just to see more clearly how we can refine the weights with each training example.
Next time we'll have to work out how to do this with a more complex network, with hidden layers.
Friday 13 March 2015
Backpropagation Part 1/3
Backpropagation is the core idea behind training neural networks. For some it's an easy algorithm to understand, for others none of the many many texts and online explanations seem to make it clear.
We'll try to talk through the idea in simple terms, to get the overall gist, and then later in a second post we'll consider some of the details.
Backpropagation Overview
The main idea is this, and it really is this simple:
In slightly more detail:
Look at the following diagram showing an input layer of nodes (A, B), an internal so-called hidden layer (C, E) and an output node (F). The diagram also shows the weights between the nodes, for example WAC for the weight between node A and C. Also feeding into C is node B with weight WBC.
Now the question that took me ages to find the answer to is this: Given the error in the output of the network, how do you use this error to update the internal weights. I understood you needed to, of course, but not exactly how. Do you only update one weight? Do you consider the error out of internal nodes to be this same error from the entire neural network?
There are probably other ways to refine the network weights, but one way - the backpropagation algorithm - splits the error in proportion to the weights. So if WCF is twice as large as WEF then it should take twice as much of the error. If the error was, say 6, then WCF should be updated as if the error from C was 4, and WEF updated as if the error from E was 2 - because 4 is twice 2.
We'll look at how we actually update weight itself in the next part 2 of this blog. For now, we just want to understand the overall approach.
The above and below diagrams show the same idea then applied to nodes further back from the final output and error.
Once the error has been propagated back from the output layer back through the middle (known as "hidden", silly name) layers, and back to the weights from the input layers - we have completed a training session. Of course training needs to happen with lots of examples, which has the effect of slowly but surely refining the weights of the neural network to a point where the neural network gets better and better at predicting the right output.
Next time we'll look at the detail of using the error to update a weight. That involves some mathematics, but we'll introduce it gently.
We'll try to talk through the idea in simple terms, to get the overall gist, and then later in a second post we'll consider some of the details.
Backpropagation Overview
The main idea is this, and it really is this simple:
- We refine (train) a neural network by using example data (training data) where for each example we know the question (input) and the answer (output).
- For each example we use the error - the difference between the right answer and what the neural network outputs - to determine how much we refine the internals of the neural network.
- We keep doing this for other examples, until we're happy that the neural network gets enough answers right, or close enough.
In slightly more detail:
- We start with an untrained network, and a training set of examples to learn from - which consists of inputs and the desired outputs.
- To train the network we apply the input of each example to the untrained network. This could be the human handwritten characters we're interested in for our project.
- The untrained network will, of course, produce an output. But because it is untrained, the output is very likely incorrect.
- We know what the output should be, because we're using a training example set. We can compare the desired output with the actual but incorrect output - that's the error.
- Rather than disregard this error - we use it because it gives us a clue as to how to refine the neural network to improve the output. This refinement is done by adjusting the "weights" in the network, which we saw in an earlier post.
Look at the following diagram showing an input layer of nodes (A, B), an internal so-called hidden layer (C, E) and an output node (F). The diagram also shows the weights between the nodes, for example WAC for the weight between node A and C. Also feeding into C is node B with weight WBC.
Now the question that took me ages to find the answer to is this: Given the error in the output of the network, how do you use this error to update the internal weights. I understood you needed to, of course, but not exactly how. Do you only update one weight? Do you consider the error out of internal nodes to be this same error from the entire neural network?
There are probably other ways to refine the network weights, but one way - the backpropagation algorithm - splits the error in proportion to the weights. So if WCF is twice as large as WEF then it should take twice as much of the error. If the error was, say 6, then WCF should be updated as if the error from C was 4, and WEF updated as if the error from E was 2 - because 4 is twice 2.
We'll look at how we actually update weight itself in the next part 2 of this blog. For now, we just want to understand the overall approach.
The above and below diagrams show the same idea then applied to nodes further back from the final output and error.
Once the error has been propagated back from the output layer back through the middle (known as "hidden", silly name) layers, and back to the weights from the input layers - we have completed a training session. Of course training needs to happen with lots of examples, which has the effect of slowly but surely refining the weights of the neural network to a point where the neural network gets better and better at predicting the right output.
Next time we'll look at the detail of using the error to update a weight. That involves some mathematics, but we'll introduce it gently.
Sunday 1 March 2015
The MNIST Dataset of Handwitten Digits
In the machine learning community common data sets have emerged. Having common datasets is a good way of making sure that different ideas can be tested and compared in a meaningful way - because the data they are tested against is the same.
You may have come across the famous iris flower dataset which is very common for clustering or classification algorithms.
With our neural network, we eventually want it to classify human handwritten numbers. So we'd want to train it on a dataset of handwritten numbers, with labels to tell us what the numbers should be. There is in fact a very popular such dataset called the MNIST dataset. It's a big database, with 60,000 training examples, and 10,000 for testing.
The format of the MNIST database isn't the easiest to work with, so others have created simpler CSV files, such as this one. The CSV files are:
The format of these is easy to understand:
You may have come across the famous iris flower dataset which is very common for clustering or classification algorithms.
With our neural network, we eventually want it to classify human handwritten numbers. So we'd want to train it on a dataset of handwritten numbers, with labels to tell us what the numbers should be. There is in fact a very popular such dataset called the MNIST dataset. It's a big database, with 60,000 training examples, and 10,000 for testing.
The format of the MNIST database isn't the easiest to work with, so others have created simpler CSV files, such as this one. The CSV files are:
- CSV training set http://www.pjreddie.com/media/files/mnist_train.csv
- CSV test set http://www.pjreddie.com/media/files/mnist_test.csv
The format of these is easy to understand:
- The first value is the "label", that is, the actual digit that the handwriting is supposed to represent, such as a "7" or a "9". It is the answer to which the neural network is aspiring to classify.
- The subsequent values, all comma separated, are the pixel values of the handwritten digit. The size of the pixel array is 28 by 28, so there are 784 values after the label.
These files are still big, and it would be nicer to work with much smaller ones whilst we experiment and develop our code for visualising handwriting and the neural networks themselves.
So here are smaller versions of the above CSV files, but with 100 training and 10 test items:
Next we'll try to load these files into python and see if we can display the handwritten characters.
We can load the data easily from a file as follows:
f = open("mnist_test_10.csv", 'r')
a = f.readlines()
f.close()
We can then split each line according the commas, to get the label and the bitmap values, from which we build an array. We do need to reshape the linear array to 28x28 before we display it.
f = figure(figsize=(15,15));
count=1
for line in a:
linebits = line.split(',')
imarray = numpy.asfarray(linebits[1:]).reshape((28,28))
subplot(5,5,count)
subplots_adjust(hspace=0.5)
count += 1
title("Label is " + linebits[0])
imshow(imarray, cmap='Greys', interpolation='None')
pass
The output in IPython is a series of images, You can check that the label matches the handwritten image:

We can load the data easily from a file as follows:
f = open("mnist_test_10.csv", 'r')
a = f.readlines()
f.close()
We can then split each line according the commas, to get the label and the bitmap values, from which we build an array. We do need to reshape the linear array to 28x28 before we display it.
f = figure(figsize=(15,15));
count=1
for line in a:
linebits = line.split(',')
imarray = numpy.asfarray(linebits[1:]).reshape((28,28))
subplot(5,5,count)
subplots_adjust(hspace=0.5)
count += 1
title("Label is " + linebits[0])
imshow(imarray, cmap='Greys', interpolation='None')
pass
The output in IPython is a series of images, You can check that the label matches the handwritten image:
Cool - we can now import handwritten image data from the MNIST dataset and work with it in Python!
PS Yes, the "subplots" command for each loop isn't efficient but I didnt' have time to work out how to do plotting subplots properly.
UPDATE: The book is out! - and provides examples of working with the MNIST data set, as well as using your own handwriting to create a test dataset.
UPDATE: The book is out! - and provides examples of working with the MNIST data set, as well as using your own handwriting to create a test dataset.
Sunday 11 January 2015
Why Activation Functions must be Non-Linear?
In the previous post we looked at the basic of a neural network, the node, and how it works. For simplicity we used a linear function for the activation function - but for real neural networks we can't do this.
Why not? Let's step through the reasoning step by step.
Q1: Why do we need many nodes, arranged in a mesh?
Now, let's go back to our first question.
Q2: Why do we need activation functions to be non-linear?
Why isn't a simple linear function like y=ax+b not useful?
The reason is that the overall effect of a neural network, composed of nodes with simple linear functions, is itself a simple linear function. You've lost the benefit of having lots of nodes, and the benefit of arranging them in a mesh. You may as well just have a single node, because you don't have any more expressive power than a single node.
How is this shocking conclusion be possible?
If you consider any single node in a mesh of nodes, all it is doing is taking a linear combination of the outputs from other nodes and applying the activation function to arrive at its output. The linear combination is simply the weighted sum we are familiar with. If the activation function is linear too, then the output is a linear function of the outputs of the nodes which feed into it. That is output = linear_function(inputs).
Now if we expand our thinking from one node to nodes, we have the output of the seconf node as being a linear function of the output of the first node, which itself was a linear combination of that first node's input. So the overall output is still linear with the inputs.
If we keep going with this thinking, expanding out mental picture to more nodes, even connected as a mesh, we find that the overall output from a neural network is a linear function of the network's inputs. And this can be modelled with a single node.
So a network of nodes is equiavalent to a single node if the activation function is linear. And so you can't learn to model anything more complex than a single node with a linear activation function.
This reduction isn't possible if the activation function is non-linear. Normally we like things to be simple and reducible, but here we don't because the upheld complexity is what is needed to ensure the network can model more complex worlds.
Just to be super-clear .. a function of a function - f(f(x)) is linear if f is linear. And it's not linear if f is not linear. Linear functions are a special case.
To illustrate:
The sigmoid function commonly used for neural networks 1/(1+exp(-x)) is similarly non-linear.
Why not? Let's step through the reasoning step by step.
Q1: Why do we need many nodes, arranged in a mesh?
- We don't have a neural network of just one node, we have many, often arranged into layers. This is because a single node has limited expressive power - it can't do more than it's activation function allows it to. If that activation function is a simple linear y=ax+b then all it will ever do is learn to separate the world into two by a straight line. Even a more complex sigmoid activation function will only ever separate the world by a single line, albeit curved like a sigmoid.
- So one node is not enough. Perhaps many nodes can together, as a network, learn to model the world in a more sophisticated complex ways? The answer is yes if you connect them as a network, with layers of nodes. The answer is no if you simply line them up, connected serially one after another. So the arrangement - the topology - of a neural network matters.
- OK - so we've established that the nodes must be connected as a mesh, or web, to stand a chance of modelling modelling a world more complex than the individual activation functions could allow.
Now, let's go back to our first question.
Q2: Why do we need activation functions to be non-linear?
Why isn't a simple linear function like y=ax+b not useful?
The reason is that the overall effect of a neural network, composed of nodes with simple linear functions, is itself a simple linear function. You've lost the benefit of having lots of nodes, and the benefit of arranging them in a mesh. You may as well just have a single node, because you don't have any more expressive power than a single node.
How is this shocking conclusion be possible?
If you consider any single node in a mesh of nodes, all it is doing is taking a linear combination of the outputs from other nodes and applying the activation function to arrive at its output. The linear combination is simply the weighted sum we are familiar with. If the activation function is linear too, then the output is a linear function of the outputs of the nodes which feed into it. That is output = linear_function(inputs).
Now if we expand our thinking from one node to nodes, we have the output of the seconf node as being a linear function of the output of the first node, which itself was a linear combination of that first node's input. So the overall output is still linear with the inputs.
If we keep going with this thinking, expanding out mental picture to more nodes, even connected as a mesh, we find that the overall output from a neural network is a linear function of the network's inputs. And this can be modelled with a single node.
So a network of nodes is equiavalent to a single node if the activation function is linear. And so you can't learn to model anything more complex than a single node with a linear activation function.
This reduction isn't possible if the activation function is non-linear. Normally we like things to be simple and reducible, but here we don't because the upheld complexity is what is needed to ensure the network can model more complex worlds.
Just to be super-clear .. a function of a function - f(f(x)) is linear if f is linear. And it's not linear if f is not linear. Linear functions are a special case.
To illustrate:
- If f(x) = ax+b .. then f(f(x)) = a(ax+b) + b = a2x + ab + b .. still linear with respect to the input x.
- However if f(x) is non-linear f(x) = ax2 + bx + c then f(f(x)) = a(ax2+ bx + c)2 + b(ax2+bx+c) + c which is of the order x4 .. definitely not linear.
- Linear functions are a special case .. a function of a function of a function .. etc .. f(f(f(f(...)))) is linear only f is linear.
The sigmoid function commonly used for neural networks 1/(1+exp(-x)) is similarly non-linear.
Sunday 4 January 2015
The Workings of A Neural Node
It's always worth breaking complex things down into simpler things.
Neural networks are made up of nodes, which all behave in roughly the same way. The following diagram shows a node, and shows what's going on (click to enlarge):
The input is just whatever is incoming to that neural node. It could be input from the outside world, the stimulus against which the neural network is workign on, or the output from another node inside the neural network.
The output is the signal that the node pushes out, after having gone through a few steps, which we'll talk about next. The output could be part of the final set of answers that the whole neural network emits, or it could go to another node as that node's input.
To calculate the output, the node could be really simple and just pass the input through unmodified. That would be ok but it wouldn't be a useful node - it's existence wouldn't be needed. So the node needs to do something.
The first thing the node does is apply a weight to the input. This is usually done by simply multiplying the input by a number to redue or magnify it. This is particularly useful when a node has many inputs (from stumuli or from other nodes) and each is weighted individually to give some more importance than others.
The node takes the input, modified by the weight, and applies an activation function to it before emitting the result as its output. This could be any function but becuase neural networks were inspired by biological brains, the function is usually one which tries to mimic how real neurons would work. Real neurons appear not to fire if the input isn't large enough. They only fire once the input is strong enough. A step function, like the Heaviside step function, would seem to be good enough, but because the maths involved when training a neural network, the smoother sigmoid function is used. What's more the smoother sigmoid function is closer to how a biological system responds, compared to the square unnatural robotic step function.
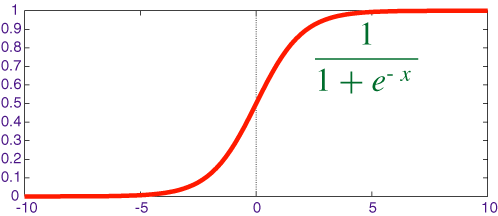
The following is a visual representation of a sigmoid function from here. Don't worry too much about the mathematical expression for now. You can see that for low input values (horizontal axis) the responce is zero, and for high input values the responce is 1, with a gradual smooth natural transition between the two.
It's always much easier to see an example working:
Neural networks are made up of nodes, which all behave in roughly the same way. The following diagram shows a node, and shows what's going on (click to enlarge):
The input is just whatever is incoming to that neural node. It could be input from the outside world, the stimulus against which the neural network is workign on, or the output from another node inside the neural network.
The output is the signal that the node pushes out, after having gone through a few steps, which we'll talk about next. The output could be part of the final set of answers that the whole neural network emits, or it could go to another node as that node's input.
To calculate the output, the node could be really simple and just pass the input through unmodified. That would be ok but it wouldn't be a useful node - it's existence wouldn't be needed. So the node needs to do something.
The first thing the node does is apply a weight to the input. This is usually done by simply multiplying the input by a number to redue or magnify it. This is particularly useful when a node has many inputs (from stumuli or from other nodes) and each is weighted individually to give some more importance than others.
The node takes the input, modified by the weight, and applies an activation function to it before emitting the result as its output. This could be any function but becuase neural networks were inspired by biological brains, the function is usually one which tries to mimic how real neurons would work. Real neurons appear not to fire if the input isn't large enough. They only fire once the input is strong enough. A step function, like the Heaviside step function, would seem to be good enough, but because the maths involved when training a neural network, the smoother sigmoid function is used. What's more the smoother sigmoid function is closer to how a biological system responds, compared to the square unnatural robotic step function.
The following is a visual representation of a sigmoid function from here. Don't worry too much about the mathematical expression for now. You can see that for low input values (horizontal axis) the responce is zero, and for high input values the responce is 1, with a gradual smooth natural transition between the two.
It's always much easier to see an example working:
- Let's imagine we have a really simple activation function f(x) = x2 to keep this example clear.
- Let's imagine we have only one input, and that is 0.5.
- The weight is set to 0.8
- So the weighted input is 0.5 * 0.8 = 0.4
- The activation function f(x) = x2 becomes 0.42 = 0.16, that's the output.
Friday 2 January 2015
Welcome!
Welcome to Make Your Own Neural Network!
This blog will follow the development of my new ebook on neural networks, discuss interesting ideas and your feedback.
My previous ebook Make Your Own Mandelbrot was a surprising success, and this ebook will follow the same core philosophy: to take a gentle journey through the mathematical concepts needed to understand neural networks, and also to introduce just enough Python to make your own.
The critical thing for me is to be able to explain the ideas in a way that any teenager can understand - because I really believe too any other guides unnecessarily put people off with their terrible explanations and jargon.
You can follow the other blog at http://makeyourownmandelbrot.blogspot.co.uk/ and on twitter @myomandelbrot
This blog will follow the development of my new ebook on neural networks, discuss interesting ideas and your feedback.
My previous ebook Make Your Own Mandelbrot was a surprising success, and this ebook will follow the same core philosophy: to take a gentle journey through the mathematical concepts needed to understand neural networks, and also to introduce just enough Python to make your own.
The critical thing for me is to be able to explain the ideas in a way that any teenager can understand - because I really believe too any other guides unnecessarily put people off with their terrible explanations and jargon.
You can follow the other blog at http://makeyourownmandelbrot.blogspot.co.uk/ and on twitter @myomandelbrot
Subscribe to:
Posts (Atom)











.png)